
1. 一项工作,如果单独完成,甲需要20小时,乙需要24小时,丙需要30小时。现在三人合作,甲中途因事请假,结果用了12小时完成。甲工作了( )小时。
A. 6 B. 4
C. 2 D. 1
2. 小明计划40天完成一项工作,开工后10天完成了全部工作的,接着干了15天完成了剩余工作量的 ,最后几天的工作效率与原计划的工作效率相间,问小明实际做了多少天?
,最后几天的工作效率与原计划的工作效率相间,问小明实际做了多少天?
A. 25 B. 29
C. 31 D. 35
3. 甲、乙各负责A、B两个工程,甲完成A的时间是12天,乙完成B工程的时间是15天,雨天甲的工作效率降低40%,乙的工作效率降低10%,甲乙同时完成工程。问晴天有几天?
A. 4 B. 5
C. 6 D. 8
4. 有一项商业设计绘图任务,若交给甲一人单独绘制,需要15天完成;若交给甲、乙两人合作绘制,需要8天完成;若交给乙、丙两人合作绘制,需要10天完成。如果现在交给三人一起合作完成这项绘图任务,则需要( )天。
A. 4 B. 5
C. 6 D. 7
5. 现有某项工程,小张单独完成需要10天,小李单独完成需要15天,如果两人联手做,需要多少天完成?
A. 8 B. 7
C. 6 D. 5
6. 生产一批产品,甲单独工作需要10天完成,乙单独工作需要4天完成。现在先由甲工作5天,剩下的工作交给乙继续完成。则乙需要再做( )天可以完成全部工作。
A.4 B.3
C.2 D.1
7. 某工厂生产一批零件,甲、乙两队合作需要6天完成,乙、丙两队合作需要12天完成,甲、丙两队合作需要8天完成。则甲、乙、丙三队合作在()天内能完成。
A. 6 B. 7
C. 8 D. 9
8. 一片棉田,甲队单独摘棉花用20天的时间可以摘完,乙队单独摘棉花用10天的时间可以摘完,现在甲乙两队轮替摘棉花。问:摘完整片棉田需要多少天?
A. 13 B. 14
C. 15 D. 16
9. 某公司一项任务交由甲乙两个小组完成,甲组单独15天可完成,乙组单独10天可完成。现甲组先单独进行5天,然后两组合作,还需要多少天能完成剩余任务:
A. 4天 B. 5天
C. 6天 D. 7天
10. 一个工程给甲单独做12个小时完成,给乙单独做6小时完成,给丙单独做4小时完成,已知该工程先由甲和乙共同先做1小时,剩下的由丙来做,那么丙做完这个工程还需要()小时。
A. 2 B. 3
C. 3.5 D. 4
答案解析...请翻下一页哦~
| 2024云南省事业单位备考推荐 | |
| 2024下半年云南事业单位公告预约 | 云南事业单位职位在线查询 |
| 2024云南事业单位全省岗位表下载 | 云南事业单位考试专题信息网 |
| 2024云南事业单位联考图书4本套 | 2024云南事业单位D类4本套 |
| 2024云南事业单位联考必做题库 | 2024事业单位D类必做题库 |

1.【答案】C
【解析】第一步,本题考查工程问题,属于给定时间类。
第二步,赋值工程总量为120(20、24、30的公倍数),那么甲的效率为6,乙的效率为5,丙的效率为4。设甲工作了x小时,由三人合作,甲中途因事请假,结果用了12小时完成,列方程得:6x+(4+5)×12=120,解得x=2(小时)。
因此,选择C选项。
2.【答案】D
【解析】第一步,本题考查工程问题,属于给定时间类。
第二步,由题干“小明计划40天完成一项工作,开工后10天完成了全部工作的 ,接着干了15天完成了剩余工作量的
,接着干了15天完成了剩余工作量的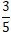 ”,赋值工作总量为200(40、25的最小公倍数),则小明的原计划效率为200÷40=5;开工后10天完成了全部工作的
”,赋值工作总量为200(40、25的最小公倍数),则小明的原计划效率为200÷40=5;开工后10天完成了全部工作的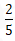 ,完成工作量为200×
,完成工作量为200× =80,接着干了15天完成了剩余工作量的
=80,接着干了15天完成了剩余工作量的 ,完成工作量为(200-80)×
,完成工作量为(200-80)×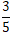 =72。
=72。
第三步,最后剩余的工作量需要完成的时间为:(200-80-72)÷5=9.6(天),因此小明实际做了10+15+9.6=34.6(天),取整35天。
因此,选择D选项。
3.【答案】C
【解析】第一步,本题考查工程问题。

【拓展】A、B两工程工作总量并不一定相等,这里都设单位“1”,是因为在方程中A的工作量、B的工作量都约分掉,所以都设单位“1”对结果没有影响。
4.【答案】C
【解析】第一步,本题考查工程问题,属于给定时间类。
第二步,由题干“甲一人单独绘制,需要15天完成;若交给甲、乙两人合作绘制,需要8天完成;若交给乙、丙两人合作绘制,需要10天完成”,赋值工作总量为120(15、8和10的最小公倍数),则甲的效率为120÷15=8,甲、乙效率和为120÷8=15,乙、丙效率和为120÷10=12,三人的效率和为8+12=20。
第三步,交给三人一起合作完成这项绘图任务,则需要120÷20=6(天)。
因此,选择C选项。
5.【答案】C
【解析】第一步,本题考查工程问题,属于给定时间型。
第二步,赋值工程总量为10和15的公倍数30,则小张和小李的效率各为3和2;如果两人联手做,需要30÷(3+2)=6(天)。
因此,选择C选项。
6.【答案】C
【解析】第一步,本题考查工程问题,属于给定时间类。
第二步,赋这一批产品的总工作量为40,则甲每天的效率为4,乙每天的效率为10。现在甲工作5天的工作量=5×4=20,还剩下工作量=40-20=20,由乙继续完成。
第三步,解得乙需要再做的天数=20÷10=2天。
因此,选择C选项。
7.【答案】A
【解析】第一步,本题考查工程问题,属于给定时间类。
第二步,根据工作总量=工作时间X工作效率,赋工作总量为24(6和12的公倍数),则甲加乙的工作效率为4,乙加丙的工作效率为2,甲加丙的工作效率为3,那么甲、乙、丙的工作效率为(4+2+3)2=4.5,三队合作完成需要的天数为244.5≈5.3(天),因此6天内可以完成。
因此,选择A选项。
8.【答案】B
【解析】第一步,此题考查工程问题,属于给定时间类。
第二步,根据工作总量=工作时间×工作效率,赋工作总量为20(20和10的公倍数),可得甲队效率为1,乙队效率为2。现在两队轮替摘棉花,那么每两天的工作效率是甲队和乙队效率之和,即1+2=3,20÷3=6……2,需要6个2天,即12天,剩余2个工作量,需要甲做一天,乙做一天才能做完。所以一共需要12+2=14(天)。
因此,选择B选项。
9.【答案】A
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法解题。
第二步,赋工作总量为30(15和10的公倍数),则甲组工作效率为2,乙组工作效率为3。甲先单独进行5天后,还剩工作量30-(5×2)=20,然后两组合作,则还需要的天数为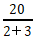 =4(天)。
=4(天)。
因此,选择A选项。
10.【答案】B
【解析】第一步,本题考查工程问题,属于给定时间类。
第二步,赋工作总量为12(12、6、4的公倍数),则甲的效率是每小时1,乙的效率是每小时2,丙的效率是每小时3。先由甲和乙共同做1小时,则剩余工作量为12-(1+2)×1=9,剩下的由丙来做,那么丙还需要做9÷3=3(小时)。
因此,选择B选项。










