在整场考试还剩十分钟的时候,为了扭转人生局势你还是放心不下地瞄了一眼数量关系,于是你开始庆幸自己多看了一眼,跃然纸上的是多么熟悉的配方。

下面是课上讲过的数量关系例题:

下面是2019年国考省部级数量关系中神一致考题:
2019年国家省部级-64(题目来自考生回忆)
一个圆形的人工湖,直径为50公里,某游船从码头甲出发,匀速直线行驶30公里到码头乙停留36分钟,然后到与码头甲直线距离为50公里的码头丙,共用时2小时。问该游船从码头甲直线行驶到码头丙需用多少时间?
A.50分钟 B.1小时
C.1小时20分 D.1小时30分
【答案】B
【解析】甲丙之间的距离为50公里,则甲丙为一条直径的两端,如下图:
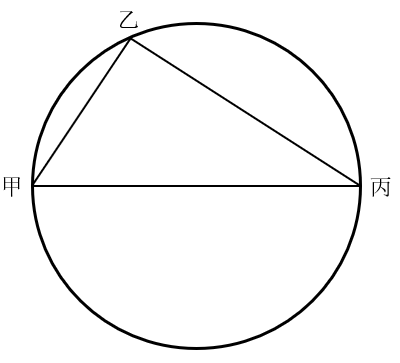
已知“圆上任意一点与直径构成的三角形为直角三角形”,则甲乙丙构成直角三角形,又甲乙间距离为30公里,甲丙间距离为50公里,利用勾股定理可知,乙丙间距离为40公里,甲—乙—丙行驶30+40=70公里,用时120-36=84分钟,平均每公里用时84÷70=1.2分钟,甲直线行驶到丙50公里需用时:50×1.2=60分钟=1小时。因此,选择B选项。
下面是课上讲过的数量关系例题:

下面是2019年国考省部级数量关系中神一致考题:
2019年国家省部级-66(题目来自考生回忆)
A和B两家企业2018年共申请专利300多项,其中A企业申请的专利中27%是发明专利,B企业申请的专利中,发明专利和非发明专利之比为8:13。已知B企业申请的专利数量少于A企业,但申请的发明专利数量多于A企业。问两家企业总计最少申请非发明专利多少项?
A.237 B.242
C.250 D.255
【答案】A
【解析】A、B两家企业共申请专利300多项,B的专利数量少于A,A企业申请的专利总共27%是发明专利,可知A申请的总数为100的倍数,则A申请的总数为200项,A中发明为200×27%=54项,B中发明与非发明之比为8:13,设B中发明与非发明分别为:8x和13x项,8x>54,且要使总申请数尽量少,则x=7,A中非发明为:200×(1-27%)=146项;B中非发明为:13×7=91项,两家企业总计最少申请非发明专利146+91=237项。因此,选择A选项。
下面是课上讲过的数量关系例题:

下面是2019年国考地市级数量关系中神一致考题:
2019年国家地市级-65(题目来自考生回忆)
甲和乙进行5局3胜的乒乓球比赛,甲每局获胜的概率是乙每局获胜概率的1.5倍。问以下哪种情况发生的概率最大?
A.比赛在3局内结束 B.乙连胜3局获胜
C.甲获胜且两人均无连胜 D.乙用4局获胜
【答案】A
【解析】由甲获胜的概率是乙获胜概率的1.5倍可得,甲获胜概率为60%,乙获胜的概率是40%。则A选项的概率为0.63+0.43,B选项的概率为0.43,C选项的概率为0.63×0.42,D选项的概率为C3 4×0.43×0.6-0.43=1.4×0.43,比较大小可得A最大。因此,选择A选项。

开心那么大,提高一分,干掉千人。其实,就算是你最紧张的数量关系,也是有很多知识点都是曾经学过的,如果你给数量十分钟,分数就够逆天啦!

下面是课上讲过的数量关系例题:

下面是2019年国考省部级数量关系中神一致考题:
2019年国家省部级-64(题目来自考生回忆)
一个圆形的人工湖,直径为50公里,某游船从码头甲出发,匀速直线行驶30公里到码头乙停留36分钟,然后到与码头甲直线距离为50公里的码头丙,共用时2小时。问该游船从码头甲直线行驶到码头丙需用多少时间?
A.50分钟 B.1小时
C.1小时20分 D.1小时30分
【答案】B
【解析】甲丙之间的距离为50公里,则甲丙为一条直径的两端,如下图:

已知“圆上任意一点与直径构成的三角形为直角三角形”,则甲乙丙构成直角三角形,又甲乙间距离为30公里,甲丙间距离为50公里,利用勾股定理可知,乙丙间距离为40公里,甲—乙—丙行驶30+40=70公里,用时120-36=84分钟,平均每公里用时84÷70=1.2分钟,甲直线行驶到丙50公里需用时:50×1.2=60分钟=1小时。因此,选择B选项。
下面是课上讲过的数量关系例题:

下面是2019年国考省部级数量关系中神一致考题:
2019年国家省部级-66(题目来自考生回忆)
A和B两家企业2018年共申请专利300多项,其中A企业申请的专利中27%是发明专利,B企业申请的专利中,发明专利和非发明专利之比为8:13。已知B企业申请的专利数量少于A企业,但申请的发明专利数量多于A企业。问两家企业总计最少申请非发明专利多少项?
A.237 B.242
C.250 D.255
【答案】A
【解析】A、B两家企业共申请专利300多项,B的专利数量少于A,A企业申请的专利总共27%是发明专利,可知A申请的总数为100的倍数,则A申请的总数为200项,A中发明为200×27%=54项,B中发明与非发明之比为8:13,设B中发明与非发明分别为:8x和13x项,8x>54,且要使总申请数尽量少,则x=7,A中非发明为:200×(1-27%)=146项;B中非发明为:13×7=91项,两家企业总计最少申请非发明专利146+91=237项。因此,选择A选项。
下面是课上讲过的数量关系例题:

下面是2019年国考地市级数量关系中神一致考题:
2019年国家地市级-65(题目来自考生回忆)
甲和乙进行5局3胜的乒乓球比赛,甲每局获胜的概率是乙每局获胜概率的1.5倍。问以下哪种情况发生的概率最大?
A.比赛在3局内结束 B.乙连胜3局获胜
C.甲获胜且两人均无连胜 D.乙用4局获胜
【答案】A
【解析】由甲获胜的概率是乙获胜概率的1.5倍可得,甲获胜概率为60%,乙获胜的概率是40%。则A选项的概率为0.63+0.43,B选项的概率为0.43,C选项的概率为0.63×0.42,D选项的概率为C3 4×0.43×0.6-0.43=1.4×0.43,比较大小可得A最大。因此,选择A选项。

开心那么大,提高一分,干掉千人。其实,就算是你最紧张的数量关系,也是有很多知识点都是曾经学过的,如果你给数量十分钟,分数就够逆天啦!









