在数量关系中,经常出现一些需要我们寻找规律,总结规律并使用规律的题目,这时候,就需要使用枚举归纳法来解决。
枚举归纳法在数学运算中是一个重要的解题思想, 尤其在国家公务员的考试中, 好多题目可以通过此方法来求解。在题目中, 有些题, 看似并没有什么思路, 很繁琐的题目, 我们举几个例子就可以解决, 这就是枚举归纳法的玄妙之处。枚举是将所有可能出现的情况逐个列举。而归纳, 是通过最初的枚举罗列出第一步、第二步、第三步, 然后探索、猜测出隐藏的规律。
枚举归纳法作为一种非常实用的方法,也越来越多的成为我们解决一些复杂问题的法宝秘籍,比如下面这几个题:
【例1】(2018军队文职)公司小张、小王、小李、小陈4 人在工作日轮流值班,每周五值班员要撰写一周小结。3月5日周五小李值班撰写了小结,下一次小李撰写一周小结的日期是:
A 4月9日
B4月2日
C 3月29日
D3月23日
【答案】B
【解析】第一步,本题考查星期日期问题。用枚举法解题。
第二步,小张、小王、小李、小陈四人工作日轮流值班,形成一个周期,3月5日周五小李值班撰写总结,利用枚举法,情况如下表:
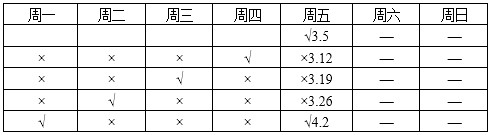
故下一次小李撰写一周小结的日期是4月2日。
因此,选择B选项。
【例2】(2019联考)某技校在每月首日招收学员,学习时限以月为周期,每月首日为考核日,考核通过即离校。每批学员学习1个月后, 在次月初考核通过的比例为10%,而学习2个月后,仍未通过考核的占该批学员的50%,学习3个月后该批学员全部考核通过离校。如果从3月份起,该技校开始招收学员且每个月招收300名学员,则同年7月2日在该技校的学员有多少名?
A 540
B 600
C 720
D 810
【答案】C
【解析】第一步,本题考查基础应用题,用枚举法解题。
第二步,根据题目描述,列出下表:
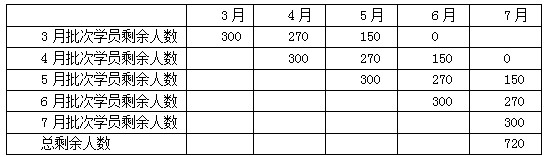
同年7月2日该技校学员的总数,包括5月批次学员剩余的150名,6月批次学员剩余的270名,7月批次学员剩余的300名,那么共有学生150+270+300=720(名)。
因此,选择C选项。

扫码领取国考白皮书(国考考情考务解读)
【例3】(2021江苏ABC)某公司举办迎新晚会,参加者每人都领取一个按入场顺序编号的号牌,晚会结束时宣布:从1号开始向后每隔6个号的号码可获得纪念品A,从最后一个号码开始向前每隔8个号的号码可获得纪念品B。最后发现没有人同时获得纪念品A和B,则参加迎新晚会的人数最多有:
A 46人
B 48 人
C 52人
D 54人
【答案】B
【解析】第一步,本题考查循环周期问题,用枚举法解题。
第二步,获得纪念品A的编号分别为:1、8、15、22、29、36、43、50……,问题所求为人数最多,从最大的选项开始依次代入:
D选项,获得纪念品B的编号分别为:54、45、36,36号同时获得纪念品A和B,排除;
C选项,获得纪念品B的编号分别为:52、43,43号同时获得纪念品A和B,排除;
B选项,获得纪念品B的编号分别为:48、39、30、21、12、3,没有人同时获得纪念品A和B,符合题意。
因此,选择B选项。
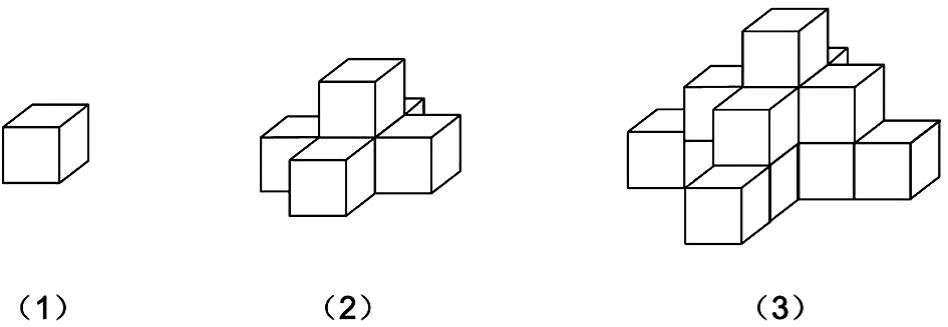
【例4】(2021上海)有若干个相同的小正方体木块, 按图(1),(2),(3)的叠放规律摆放,则到第七个图时,第七个图中小正方体木块总数应为( )个。
A 25
B 66
C 91
D 120
【答案】C
【解析】第一步,本题考查几何问题,属于几何计数类。
第二步,第一个图的小正方体有1个;第二个图比第一个图多5个有6个;第三个图比第二个图多5+4=9个,即15个;以此类推,第四个图比第三个图多9+4=13个,即28个;第五个图比第四个图多13+4=17个,即45个;第六个图比第五个图多17+4=21个,即66个;第七个图比第六个图多21+4=25个,即91个。
因此,选择C选项。
枚举归纳法这种方法有时看上去繁琐, 但是却是找不到思路时的最直观思维。常用在选项数据比较小或者题目数据过大, 无法直接计算时。适合题型有:日期推断、规律探索、几何计数/ 构造等。

| 2025年国考公告预约 | 2025年国考职位查询 |
| 2025年国考考试大纲 | 国考历年笔试合格分数线 |
| 2025年国考先学计划 | (见证)2025公考学习计划 |










