
1、某大学一年级,开设三门2分的和四门1分的选修课。要求每名学员当期选修课的分数不低于4分,则每名学员在恰好满足学分的情况下,可选择的选修课组合情况数为:
A.22种
B.21种
C.20种
D.18种
2、某省举办一年一度的运动会,各高校纷纷踊跃参加,每位选手参加各单项比赛计入所在团体总分的规则为:一等奖得分7分,二等奖得分5分,三等奖得分2分。已知甲高校共有15位参赛选手,均获奖,且甲高校最后的总分为72分,则甲高校最多有( )位选手获得一等奖。
A.6
B.3
C.5
D.7
3、舞蹈队排练一个大型节目,在队形变化的时候需要可以平均分成若干个4人组,还可以平均分成若干个6人组,还可以平均分成若干个7人组,最终排练这个节目共上了不到一百人。这些排练的队员中,男性比女性少10人,超过20岁的比不超过20岁的少20人。那么不超过20岁的男性最少有多少人?
A.2
B.3
C.4
D.5
4、30名游泳运动员轮流参加蛙泳训练,按顺序从1到3依次不重复地报数,谁数到3谁下池游泳,凡游过一次的运动员不再参加报数。当仅剩1名运动员尚未下池游泳时,问:共报数多少人次?
A.97
B.87
C.77
D.67
5、某公司给表现良好的11名职工发放一二三等奖金。奖金设置为一等奖金3000元,二等奖金2000元,三等奖金500元,一共发了15000元。求三等奖金发放给了几个人?
A.5
B.6
C.7
D.8
答案解析...请翻下一页哦~

1、【答案】A
【解析】
第一步,本题考查排列组合问题。
第二步,要求恰好满足学分,即选修4分。分情况讨论:
(1)选修两门2分选修课,情况数为:![]() =3(种);
=3(种);
(2)选修一门2分和两门1分选修课,情况数为:![]() =18(种);
=18(种);
(3)选修四门1分选修课,情况数为![]() =1(种)。
=1(种)。
则总情况数为3+18+1=22(种)。
因此,选择A选项。
2、【答案】A
【解析】
第一步,本题考查不定方程问题,用代入排除法解不定方程。
第二步,设获得一等奖的有x位选手、获得二等奖的有y位选手、获得三等奖的有z位选手。根据共15位选手参赛和总分为72分,可列不定方程组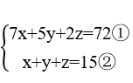 ,①-②×5可得:2x-3z=-3。
,①-②×5可得:2x-3z=-3。
第三步,问最多有几位选手获得一等奖,最值代入,优先代入D选项,x=7,z无整数解,排除;代入A选项,若x=6,z=5,y=4,满足题意。
因此,选择A选项。
3、【答案】D
【解析】
第一步,本题考查约数倍数问题。
第二步,排练总人数应为4、6、7的公倍数,最小为84,不到一百人即84人。84人中女性为(84+10)÷2=47人,超过20岁的有(84-20)÷2=32人。让女性与超过20岁尽量无重叠,则最多有47+32=79人,此时不超过20岁的男性最少,为84-79=5人。
因此,选择D选项。
4、【答案】B
【解析】
第一步,本题考查基础计算,属于循环周期类问题。
第二步,根据从1到3依次不重复地报数,可知每报数3次,会有1人下池游泳。
第三步,仅剩1名运动员尚未下池游泳时,可知已下池游泳的人数为30-1=29(人),则需报数29×3=87(人次)。
因此,选择B选项。
5、【答案】B
【解析】
第一步,本题考查不定方程问题。
第二步,假设x人获得一等奖金,y人获得二等奖金,z人获得三等奖金,根据题意可列方程:①x+y+z=11;②3000x+2000y+500z=15000。化简②式得到③6x+4y+z=30。6×①-③可得:2y+5z=36,36和2y为偶数,则5z为偶数,故z为偶数,排除A、C选项。代入B选项,若z=6,则y=3,x=11-6-3=2,满足题意。(若代入D选项,z=8,则y为负数,不合题意,排除)
因此,选择B选项。










