排列组合问题属于数量关系中特别常考的一个知识点，可单独考察，也会和概率问题以及最不利原则问题结合起来考察。是特别重要的部分，需要大家理解并掌握。我们可从以下几个部分来理解和掌握。
| ↓↓↓↓2021年公务员考试面试产品推荐↓↓↓↓ | ||
| 2021省考 考试公告 |
2021省考 面试真题 |
2021省面 笔试课程 |
一、何为排列，何为组合。
排列:从n个元素中取出m个元素，排成一列,记
。(m≤n,m与n均为自然数)
组合:从n个元素中取出m个元素，组成一组,记
。(m≤n,m与n均为自然数)
例：①从10盆不同的花中取出3盆排成一排;②从10盆不同的花中取出3盆。
对于这两种说法，我们可知第一种属于排列，第二种属于组合。而两者的区别在于第一种中挑选出来的花，花的顺序不同会出现不同的结果，比如，如果我所挑出来的花是红、白、蓝三种花，则排列之后结果可能是红白蓝、红蓝白、蓝红白……而对于第二种，我只需要挑出来，挑出来之后不用再进行排序。所以排列组合之间的区别在于是否和顺序有关，排列和顺序有关系，组合没有。
二、常用方法
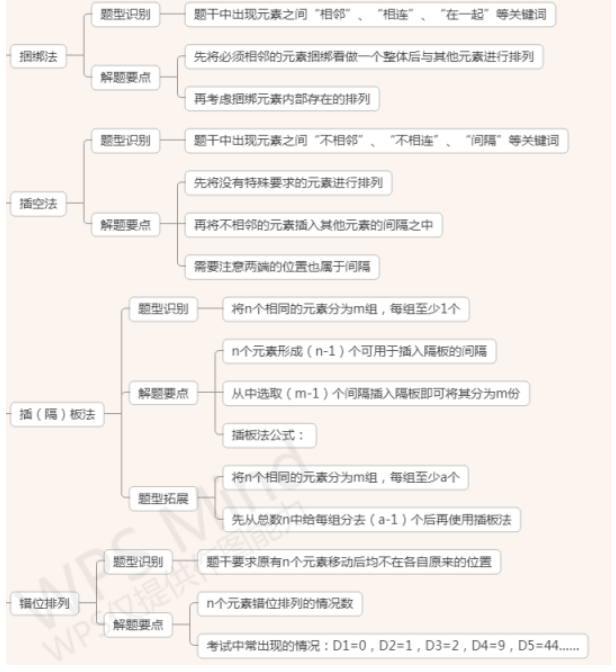
1、捆绑法:要求元素相邻时，将相邻元素捆绑在一起。
例：男生2人，女生2人，排成一排，男生必需相邻。
解析：要求男生相邻，则可以把两个男生捆在一起当做一个整体和两个女生一起排列，有A33=6种，两个男生之间还有一个内部顺序为A22=2种，则两个男生站在一起有2×6=12种。
2、插空法:要求元素不相邻时，先排好其他元素，再把不相邻元素插入其他元素所形成的空中。
例：男生2人，女生2人，排成一排，男生不能相邻。
解析：要求男生不相邻，则可以先排好两个女生有A22=4种，而两个位置周围有3个空，从三个空中挑两个空把男生安排进去，此时男生便不会相邻，有A32=6种，总的有4*6=24种。
隔板法：将n个相同元素分配给m个不同的个体，每个个体至少分得一个元素，总的分配方法有
。
例：将8个相同的橘子分配个4个不同的小朋友，一共有多少中分法?
解析：直接带入公式
=35种。
错位排列：有 n 个元素和 n 个位置，如果要求每个元素的位置与元素本身的序号都不同，在数量关系考试题中基本上只会出现五个元素的情况，所以只需要记住前五个数就可以了，其对应分别为D1=0种，D2=1种，D3=2 种，D4=9种，D5=44种。
例：一家公司有5个分公司，每个分公司派1名员工到总公司进行学习，学习完了之后不回到自己的分公司工作，请问一共有多少种分配方式?
解析：分析题目为错位排列，5个元素共有44种分配方式。
以上便是排列组合的区别以及排列组合常用的几种解题方法，希望能够帮助到各位。
图书推荐
