第一节 解题技巧

　　(一)集合的运算

　　第一步:认清集合运算符,交集运算符 “∩” ,并集运算符 “∪” ;

　　第二步:解出不等式组,在数轴上画出解集;

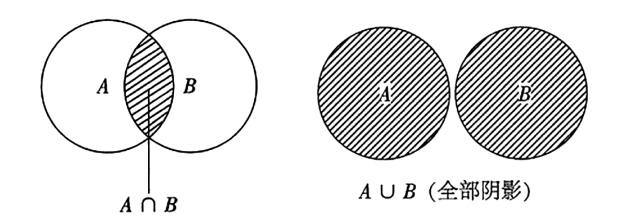
　　第三步:交集取共有部分元素,如 A ∩ B ;并集取所有元素,如 A ∪ B .

　　【例题 1】设集合 M = {x | | x - 2 | < 2} , N = {0,1,2,3,4} ,则 M ∩

　　N = ( ).

　　A. {2}

　　B. {0,1,2}

　　C. {1,2,3}

　　D. {0,1,2,3,4}

　　【答案】C

　　【解析】本题主要考查的知识点为集合的运算.

　　解得 M = {x | | x - 2 | < 2} = {x | - 2 < x - 2 < 2} = {x | 0 < x <

　　4} ,故 M ∩ N = {1,2,3} .

　　(二)充分条件、必要条件及充要条件

　　第一步:由题干条件画出逻辑推导图;

　　第二步:从左往右推满足充分性,若 A⇒B ,则 A 是 B 的充分条件,若A 不能推出 B,则 A 是 B 的不充分条件. 从右往左推满足必要性,若A⇐B ,则 A 是 B 的必要条件,若 B 不能推出 A,则 A 是 B 的不必要条件.

　　第三步:将判断出的充分性结论与必要性结论进行组合,得出答案.

　　

　　(三)函数解析式

　　第一步:换元,用新变量 t 解出 x ;

　　第二步:将函数解析式化简为 f(t) 的表达式;

　　第三步:回代,将 f(t) 的表达式中所有的 t 用 x 替换.

　　【例题 1】设函数 f(x + 1) = 2x + 2,则 f(x) = ( ).

　　A. 2x - 1

　　B. 2x

　　C. 2x + 1

　　D. 2x + 2

　　【答案】B

　　【解析】本题主要考查的知识点为求函数解析式.f(x + 1) = 2x + 2 = 2(x + 1) ,令 t = x + 1,则 x = t - 1,故 f(t) = 2t,把 t 换成 x ,因此 f(x) = 2x .

　　(四)随机事件的概率

　　第一步:用枚举法或排列组合公式写出满足条件的事件个数;

　　第二步:写出事件总个数;

　　第三步:概率 P = 发生 事 该 件 事 总 件 个 的 数 个数 .

　　【例题 1】袋中有 6 个球,其中 4 个红球,2 个白球,从中随机取出 2 个

　　球,则这 2 个球都为红球的概率为( ).