
1. 一项工程,甲乙合作,48个小时可以完成,甲单独完成需要192个小时,那么乙单独完成需要( )个小时。
A. 68 B. 72
C. 64 D. 128
2. 为了应对医用口罩紧缺情况,甲工厂和乙工厂要合作完成一批口罩的加工工作,已知甲工厂单独完成这批口罩需要15天,乙工厂需要20天,则甲乙两工厂合作至少需( )天能完成工作。
A. 6 B. 7
C. 8 D. 9
3. 某项工程由甲、乙合作6天完成,乙、丙合作的8天完成,丙、丁合作6天完成,那么由甲、乙、丙、丁四人合作()天完成该工程:
A. 3 B. 4
C. 5 D. 6
4. 两个工程队共同完成某项市政工程,蓝队单独工作需6天完成,红队单独则要3天,现在两队同时工作数天后,因红队被调走,只留蓝队,在之后的3天内完成了剩余工作量,两队共同作业的天数是:
A.1天 B.2天
C.3天 D.4天
5. 一件工程,甲队单独做15天完成,乙队单独做30天完成。现在两队合作,其间甲队休息了3天,乙队休息了6天(不存在两队同一天休息),则从开始到完工共用了:
A.9天 B.13天
C.14天 D.15天
6. 汛期来临之前,大坝需要再次加固,现在离汛期还有30天,如果甲公司来修每天需要工作12小时,如果乙公司来修每天需要工作10小时,那么两公司合作且每天只工作8小时,可以提前几天完成加固工程?
A. 8 B. 9
C. 21 D. 22
7. 假设甲、乙、丙三人单独完成一项任务依次所需的时间是6、8、12小时。现在按照甲、乙、丙、乙、丙、甲、丙、甲、乙这样顺序每人轮班工作1小时,问任务完成时,甲、乙、丙分别工作了多少小时?
A. 2、2、3 B. 3、3、2
C. 2、3、3 D. 3、2、3
8. 某市有甲乙丙三个工程队,有一个工程需要三个工程队完成合作,已知甲队单独完成这项工程需要10天,乙队单独完成这项工程需要8天,丙队单独完成这项工程需要15天。现三队合作,但甲队因故只参加了三天,丙队也休息了若干天,最后该工程用了4天完成,则丙队休息的天数是:
A. 1 B. 2
C. 3 D. 4
9. 某建筑公司准备修建一座大桥,前半部分由甲工程队完成,后半部分由乙工程队完成。在完工时,甲工程队共用了25天,乙工程队共用了30天,则甲工程队的修建速度是乙工程队的( )倍。
A. 1.2 B. 1.3
C. 1.4 D. 1.5
10. 为了应对医用口罩紧缺情况,甲工厂和乙工厂现要合作完成一批口罩的加工工作,已知甲工厂单独完成这批口罩需要15天,乙工厂需要20天,则甲乙两工厂合作至少需()天能完成工作。
A. 6 B. 7
C. 8 D. 9
答案解析...请翻下一页哦~
| 2024云南省事业单位备考推荐 | |
| 2024下半年云南事业单位公告预约 | 云南事业单位职位在线查询 |
| 2024云南事业单位全省岗位表下载 | 云南事业单位考试专题信息网 |
| 2024云南事业单位联考图书4本套 | 2024云南事业单位D类4本套 |
| 2024云南事业单位联考必做题库 | 2024事业单位D类必做题库 |

1.【答案】C
【解析】第一步,本题考查工程问题,属于时间类。

第二步,题干中只给了两个完工时间,工作总量和效率都未知,此题属于工程问题中的给定时间型,现给工作总量赋值为完工时间的最小公倍数,48和192的最小公倍数为192,所以赋值工作总量为192,进而得到甲乙合作效率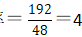 ,甲单独的效率
,甲单独的效率 ,乙单独的效率=4-3=1。
,乙单独的效率=4-3=1。
第三步,乙单独完成需要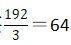 小时。
小时。
因此,选择C选项。
2.【答案】D
【解析】第一步,本题考查工程问题,属于给定时间型。
第二步,题干中已知甲乙工厂单独完工时间,工作总量和效率未知,所以本题属于给定时间型工程问题。先赋工作总量为完工时间15和20的最小公倍数,为60,即工作总量赋值为60;再得出两工厂的工作效率,甲工厂效率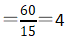 ,乙工厂效率
,乙工厂效率 。
。
第三步,甲乙两工厂合作至少需要的时间,即为两人一起做,合作时间=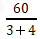 ≈8.57天,则至少需要9天。
≈8.57天,则至少需要9天。
因此,选择D选项。
3.【答案】A
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法解题。
第二步,题干中只给了3个完工时间,工作总量和效率都未知,因此属于工程问题中的给定时间型。先赋工作总量为给定时间(6、8和6)的最小公倍数,为24,即工作总量=24,再得效率:甲+乙=![]() =4,丙+丁=
=4,丙+丁=![]() =4,所以甲、乙、丙、丁四人合作的效率=4+4=8。
=4,所以甲、乙、丙、丁四人合作的效率=4+4=8。
第三步,由甲、乙、丙、丁四人合作完成该工程需要的天数=![]() =3天。
=3天。
因此,选择A选项。
4.【答案】A
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法解题。
第二步,题干中只给了两队各自的完工时间,工作总量和效率都未知。先赋工作总量为完工时间(6和3)的最小公倍数,为6,即工作总量为6,再得蓝队的工作效率= =1,红队的工作效率=
=1,红队的工作效率=![]() =2。
=2。
第三步,由红队被调走后,蓝队3天完成了剩余工作量,剩余工作量=3×1=3,则之前两队合作做了6-3=3,两队共同作业的天数=![]() =1(天)
=1(天)
因此,选择A选项。
5.【答案】C
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法解题。
第二步,题干中只给了两队各自的完工时间,工作总量和效率都未知。先赋工作总量为完工时间(15和30)的最小公倍数,为30,即工作总量为30,再得甲队的工作效率=![]() =2,乙队的工作效率=
=2,乙队的工作效率=![]() =1。
=1。
第三步,设从开始到完工共用了x天,则甲队做的天数为x-3天,乙队做的天数为x-6天,根据题意:2×(x-3)+x-6=30,解得x=14。
因此,选择C选项。
6.【答案】B
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法解题。
第二步,题干中只给了完工时间,工作总量和效率未知,属于给定时间型,甲公司完工时间=30×12=360(小时),乙公司完工时间=30×10=300(小时)。先赋工作总量为完工时间(360、300)的最小公倍数,为1800。甲公司效率=![]() =5,乙公司效率=
=5,乙公司效率=![]() =6。
=6。
第三步,两公司合作每天做8×(5+6)=88,则需要的时间=![]() ≈20.5(天),需要21天,可以提前30-21=9(天)。
≈20.5(天),需要21天,可以提前30-21=9(天)。
因此,选择B选项。
7.【答案】D
【解析】第一步,本题考查工程问题,属于给定时间类,用赋值法解题。
第二步,此题只给了甲乙丙各自的完工时间,工作总量和效率都未知,属于给定时间型工程问题。先赋工作总量为给定时间(6、8、12)的最小公倍数,为24,即工作总量为24,再得甲的效率=![]() =4,乙的效率=
=4,乙的效率=![]() =3,丙的效率=
=3,丙的效率=![]() =2。
=2。
第三步,此题的轮班做工,按照顺序每小时做的工作量累加4+3+2+3+2+4+2+4=24,做完,所以甲、乙、丙分别工作了3、2、3小时。
因此,选择D选项。
8.【答案】A
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法解题。
第二步,赋工作总量为120,工作总量=效率×时间。可根据下表求出效率关系:
| 对象 | 工作总量 | 效率 | 时间 |
| 甲 | 120 | 12 | 10 |
| 乙 | 120 | 15 | 8 |
| 丙 | 120 | 8 | 15 |
根据题干“甲队因故只参加了三天,丙队也休息了若干天,最后该工程用了4天完成”可得甲工作了3天,乙4天,丙做的工作量为120-12×3-15×4=24。丙做工的天数为24÷8=3(天)。所以丙休息的天数为4-3=1(天)
因此,选择A选项。
9.【答案】A
【解析】第一步,本题考查工程问题,属于给定时间型,利用赋值法求解。
第二步,赋值一半的工程量为150,根据,甲工程队效率为6,乙工程队效率为5。甲速度是乙的6÷5=1.2倍。
因此,选择A选项。
10.【答案】D
【解析】第一步,本题考查工程问题,属于给定时间型,用赋值法求解。
第二步,赋工作总量为120(15和20的公倍数),根据工作总量=工作效率×工作时间,又由于甲工厂单独完成这批口罩需要15天,乙工厂需要20天,则甲工厂效率为8,乙工厂效率为6。甲乙合作效率为14。合作完成需要时间为120÷148.57(天),8天完不成,至少需要9天。
因此,选择D选项。










