2022国考行测资料分析之特殊分数法有妙用
备考过行测资料分析的小伙伴都知道,资料分析想要高效拿分,用一定的速算技巧是必不可少的。那么在众多的速算技巧中,今天小编就带大家来探秘一种妙处多多的速算技巧----特殊分数法。那么,它都有哪些妙用呢?
1、巧用原则速求增长量

知道了巧解原理,那就让我们用一些近年真题来练练手吧。
【例1】2016年国产工业机器人全年累计销售29144台,较上年增长16.8%,增速较上年提升。
2016年国产工业机器人累计销售量较上年约增加了多少万台?
A.0.20
B.0.31
C.0.42
D.0.53
【答案】C
【解析】第一步,本题考查增长量计算中的已知现期量与增长率。
第二步,定位材料可知,“2016年国产工业机器人全年累计销售29144台,较上年增长16.8%”。
第三步,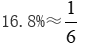 ,根据增长量计算n+1原则,则2016年国产工业机器人累计销售量较上年约增加
,根据增长量计算n+1原则,则2016年国产工业机器人累计销售量较上年约增加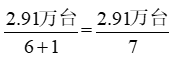 ,直除首位商4。
,直除首位商4。
因此,选择C选项。
【例2】2015年全国共建立社会捐助工作站、点和慈善超市3.0万个,比上一年减少0.2万个,其中:慈善超市9654个,同比下降5.1%。全年共接收社会捐赠款654.5亿元,其中:民政部门接收社会各界捐款44.2亿元,各类社会组织接收捐款610.3亿元。全年民政部门接收捐赠衣被4537.0万件,捐赠物资价值折合人民币5.2亿元。全年有1838.4万人次困难群众受益,同比增长8.5%,增长率较上一年下降27.5个百分点。全年有934.6万人次在社会服务领域提供了2700.7万小时的志愿服务,同比减少10.4万小时。
2015年,全国建立的慈善超市较2014年约:
A.减少519个
B.增加519个
C.减少686个
D.增加686个
【答案】A
【解析】第一步,本题考查已知现期量与增长率的增长量计算问题。
第二步,定位文字材料“2015年慈善超市9654个,同比下降5.1%”。

因此,选择A选项。
那么,特殊分数还有何妙用呢?
巧用特殊分数速算现期量

【例】按经营单位所在地分,2016年6月份,城镇消费品零售额23082亿元,同比增长10.5%;乡村消费品零售额3775亿元,同比增长11.2%。1~6月份,城镇消费品零售额134249亿元,同比增长10.2%;乡村消费品零售额21889亿元,同比增长11.0%。
按2016年1—6月份的同比增速,2017年1—6月份城镇消费品零售额约为:
A. 25506亿元
B. 172220亿元
C. 147942亿元
D. 153679亿元
【答案】C
【解析】第一步,本题考查现期量计算。
第二步,定位文字材料,“2016年1—6月份,城镇消费品零售额134249亿元,同比增长10.2%”。

还能让暴风雨来的更猛烈些吗?毕竟,学习使我快乐!
3、巧用特殊分数速算整体量
在已知部分量和比重计算整体量时,除了可以用截位直除法外,如果比重值接近某个特殊分数![]() ,此时也可以把百分数转化为特殊分数
,此时也可以把百分数转化为特殊分数![]() 来简化计算。
来简化计算。
【例】2016年,全国城市公园数量排名前五的省份依次是广东、浙江、江苏、山东和云南,公园数量分别为3512个、1171个、942个、828个和683个。其中,广东省的公园面积达65318公顷,占全国公园面积的比重超过17%;公园绿地面积达89591公顷,占全国公园绿地面积的比重约为14%。
2016年,全国公园绿地面积约为多少万公顷?
A. 64
B. 20
C. 640
D. 200
【答案】A
【解析】第一步,本题考查现期比重计算中的求整体量。
第二步,定位文字材料,“2016年,广东省公园绿地面积达89591公顷,占全国公园绿地面积的比重约为14%”。

因此,选择A选项。
最后,给大家一个小结,特殊分数常用于哪几种运算当中。
| 特殊分数法 | 在计算过程中,如果某个百分数可以转化为某个相近的特殊分数,那么就把百分数转化为这个特殊分数来简化计算 |
| 常用题型 | 求增长量、求整体量、求现期量、求部分量、求基期量等 |
那么,学到了有如此妙用的特殊分数法,相信大家现在都收获满满,跃跃欲试了。不过,想用好特殊分数法,前提还得熟练掌握好常见的特殊分数,小编就把我的经典收藏给大家奉上,一定要好好熟记和运用哦!

当然,特殊分数的妙用就仅限于此吗?当然不是,只是碍于文章篇幅有限,所以小编挑了几种常见的情形来和大家分享,其实,特殊分数的妙用无处不在,如果你想再有进一步的学习提升,咱们华图课堂见呀!
相关推荐:











