
1. 老马三年前拍下的一幅艺术大师的国画作品上涨了50%,他打算尽快出手、落袋为安。为此,他将这物按市价打八折出售,扣除成交价5%的交易费用后,老马净赚7万元。问:老马三年前拍下这幅国画时花了多少万元:
A. 38 B. 50
C. 76 D. 98
2. 有42吨货物,从甲城运往乙城,大卡车的载重量是10吨,小卡车的载重量是5吨,每种大,小卡车的耗油量分别是8升和6升,将这批货物运完,至少需要耗油:
A.35升 B.38升
C.40升 D.54升
3. 国庆期间某盆栽店进行满减活动,满50元减5元,满100元减10元,满150元减25元,满200元减30元,满250元减35元,满300减40元,满350元减50元。已知小赵买一盆盆栽花了82元,则买四盆同样的盆栽至少需要( )元。
A. 318 B. 308
C. 298 D. 288
4. 某动物园规定,个人票每张50元,团体票每张450元(可供15人游览),无其他票价优惠政策,某单位共有58人游览该动物园,则最少应付多少元?
A. 2000 B. 1800
C. 1600 D. 1500
5. 某玩具厂生产的兔子玩偶的成本是每个6元,以单价每个10元的价格批发给经销商。经销商愿意经销2000个,并且表示单价每降低0.1元,则愿意多经销200个。那么该玩具厂生产此种兔子玩偶可以获得的最大利润是:
A. 11600元 B. 11800元
C. 12200元 D. 12500元
6. 某工厂将其明星产品按质量分为8个档次。生产最低档次产品,每件获利6元,每提高一个档次,每件产品利润增加1元。用同样工时,最低档次产品每天可生产160件,每提高一个档次将减少10件。如果获利最大的产品是第R档次(最低档次为第1档次,档次依次随质量增加),那么R等于:
A. 4 B. 5
C. 6 D. 7
7. 某种产品因生产原料涨价而决定提价。现有三种提价方案:
甲:第一次提m%,第二次提n%;
乙:第一次提n%,第二次提m%;
丙:第一次提 ,第二次提
,第二次提 ;
;
m、n是不相等的正数,则这三种提价方案中:
A. 甲价格>乙价格>丙价格 B. 甲价格<乙价格<丙价格
C. 甲价格=乙价格>丙价格 D. 甲价格=乙价格<丙价格
8. 甲负费为部门聚会采购葡萄、龙眼和蓝莓三种水果,已知某水果店的葡萄11元/斤,龙眼13元/斤,蓝莓17元/斤,如果甲在该水果店正好将所带的250元钱全部用完,则甲最多可以买到( )斤水果。
A. 18 B. 20
C. 22 D. 24
9. 某电脑商城出售10种价格档位的电脑。最低价格档位的电脑每月可售出120台,每台可获利160元。每提升一个价格档位,则月销量就会减少10台,但单台利润可增加40元。若某月该电脑商城只出售某一价格档位的电脑,则当月可获得的最大利润是( )元。
A. 24000 B. 25600
C. 27040 D. 28000
10. 某人去超市买了瓜子、花生、核桃、腰果四种坚果各若干袋,共花去340元。若这些坚果每袋的价格分别为14元、22元、28元和42元,则他至少买了几袋坚果:
A. 9 B. 10
C. 11 D. 12
答案解析...请翻下一页哦~
| 2024云南省事业单位备考推荐 | |
| 2024下半年云南事业单位公告预约 | 云南事业单位职位在线查询 |
| 2024云南事业单位全省岗位表下载 | 云南事业单位考试专题信息网 |
| 2024云南事业单位联考图书4本套 | 2024云南事业单位D类4本套 |
| 2024云南事业单位联考必做题库 | 2024事业单位D类必做题库 |

1.【答案】B
【解析】解法一:
第一步,本题考查经济利润问题,属于利润折扣类,用方程法解题。
第二步,设老马买进该国画花了x万元,根据上涨50%可知市价为1.5x,打八折后成交价为1.5x×0.8=1.2x,扣除5%的交易费之后,实际售价为1.2x×(1-5%)=1.14x。
第三步,根据与买进时相比赚了7万元,可列方程1.14x-x=7,解得x=50(万元)。
因此,选择B选项。
解法二:
第一步,本题考查经济利润问题,属于利润折扣类,用赋份数解题。
第二步,赋值买进该国画花费100份,则有市价上涨50%后价格为100份×(1+50%)=150份,打八折销售,售价为150×0.8=120份,扣除5%的交易费用后,售价为120×(1-5%)=114份,利润为114-100=14份,但实际利润是7万元,两者为2倍关系,故实际成本为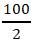 =50(万元)。
=50(万元)。
因此,选择B选项。
2.【答案】B
【解析】第一步,本题考查经济利润问题,属于统筹优化类。
第二步,本题要求运42吨固定货物的耗油最少,需要比较两种卡车的单位油耗大小,用大卡车运,每吨耗油=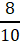 =0.8升;用小卡车运,每吨耗油=
=0.8升;用小卡车运,每吨耗油=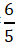 =1.2升,因此尽量多用大卡车运,耗油更少。
=1.2升,因此尽量多用大卡车运,耗油更少。
第三步,一共42吨,最优方案是:大卡车4辆,小卡车1辆。耗油4×8+1×6=38升。
因此,选择B选项。
3.【答案】C
【解析】第一步,本题考查经济利润问题,属于最值优化类。
第二步,由“小赵买一盆盆栽花了82元”,可知一盆盆栽原价=82+5=87(元),则买四盆同样的盆栽,原价=87×4=348(元)。
第三步,348满300不满350,所以不考虑满350元减50元。其他满减都统一转化成满300,分别为满300元减30元,满300元减30元,满300元减50元,满300元减45元,满300元减42元,满300减40元,所以选择满150元减25元,花钱最少,为348-50=298(元)。
因此,选择C选项。
4.【答案】B
【解析】第一步,本题考查经济利润问题,属于最值优化类。
第二步,团体票450元可供15人游览,相当于每人30元,说明团体票更划算。58人逛公园可以按60人的人数,即买4张团体票,故最少应付450×4=1800(元)。
因此,选择B选项。
【拓展】虽不足60人,但是若按58人,需要买3张团体票和13张单人票,一共需要2000元,比1800元贵。
5.【答案】D
【解析】第一步,本题考查经济利润问题,属于最值优化类。
第二步,设利润为y,单价降低x个0.1元,由经销商愿意经销2000个,并且表示单价每降低0.1元,则愿意多经销200个,列式得y=(10-6-0.1x)×(2000+200x)=200(4-0.1x)×(10+x),由一元二次函数的性质,令y=0,解得x=40或﹣10,因此当x=(40-10)÷2=15时,y取最大值,利润为200×(4-1.5)×(10+15)=12500(元)。
因此,选择D选项。
6.【答案】C
【解析】第一步,本题考查经济利润问题,属于最值优化类。
第二步,设获利最大的产品提高x个档次。由生产最低档次产品,每件获利6元,每提高一个档次,每件产品利润增加1元,那么提高x个档次后,每件利润变为(6+x)元,销量变为(160-10x)件。总利润=单个利润×销量=(6+x)×(160-10x)=10(6+x)(16-x),根据一元二次函数最值理论,当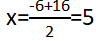 时,取最大值,即获利最大。
时,取最大值,即获利最大。
第三步,那么R=x+1=6。
因此,选择C选项。
7.【答案】D
【解析】解法一:
第一步,本题考查经济利润问题。
第二步,甲价格=原价×(1+m%)(1+n%),乙价格=原价×(1+n%)(1+m%),则甲价格=乙价格=原价×(1+m%+n%+m%×n%);丙价格=原价×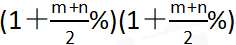 =原价
=原价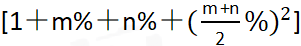 ,根据均值不等式
,根据均值不等式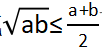 可得,当m、n不相等时,
可得,当m、n不相等时,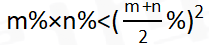 ,即甲价格=乙价格<丙价格。
,即甲价格=乙价格<丙价格。
因此,选择D选项。
解法二:
第一步,本题考查经济利润问题,用赋值法解题。
第二步,赋m=10,n=30,产品原价为100,则三种提价方案的价格分别为甲:100×1.1×1.3=143,乙:100×1.3×1.1=143,丙:100×1.2×1.2=144。D满足。
因此,选择D选项。
8.【答案】C
【解析】第一步,本题考查经济利润问题。
第二步,要想买到的水果最多,则单价最低的水果数量要尽可能多,即葡萄尽可能多买,龙眼和蓝莓尽可能少买,最少各买一斤,还剩250-(17+13)=220(元),正好可以买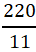 =20(斤)葡萄,故最多可买2+20=22(斤)水果。
=20(斤)葡萄,故最多可买2+20=22(斤)水果。
因此,选择C选项。
9.【答案】B
【解析】第一步,本题考查经济利润问题,属于最值优化类。
第二步,设获利最大时电脑提高x个档次,每件利润变为(160+40x)元,销量变为(120-10x)件。总利润=单个利润×销量=(160+40x)×(120-10x)=400(4+x)(12-x),根据一元二次函数最值理论,当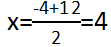 时,取最大值,即获利最大,总利润=(160+40×4)×(120-10×4)=320×80=25600(元)。
时,取最大值,即获利最大,总利润=(160+40×4)×(120-10×4)=320×80=25600(元)。
因此,选择B选项。
10.【答案】C
【解析】第一步,本题考查经济利润问题。
第二步,每袋瓜子、核桃、腰果的价格均为7的倍数,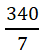 =48……4,而花生每袋价格
=48……4,而花生每袋价格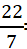 =3……1,所以至少买了4袋花生。要让买的坚果袋数最少,则要尽量多买贵的腰果。花生买了4袋,此时其他坚果共花了340—22×4=252元,每种坚果至少买一袋花14+28+42=84元,剩下的252—84=168元都买最贵的腰果,能买
=3……1,所以至少买了4袋花生。要让买的坚果袋数最少,则要尽量多买贵的腰果。花生买了4袋,此时其他坚果共花了340—22×4=252元,每种坚果至少买一袋花14+28+42=84元,剩下的252—84=168元都买最贵的腰果,能买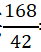 =4(袋)。所以至少买了4袋花生,瓜子、核桃各1袋,腰果1+4=5(袋),总计4+1+1+5=11(袋)。
=4(袋)。所以至少买了4袋花生,瓜子、核桃各1袋,腰果1+4=5(袋),总计4+1+1+5=11(袋)。
因此,选择C选项。










