
1.现有6个数字分别是1、2、3、4、5、6,任取两个数字组成一个两位数。现要求十位数和个位数不相等,则组成的数是偶数的概率是:

2.甲、乙、丙、丁、戊五人参加一个讲座,要求五人坐成一排,且甲只能坐在两端,则一共有( )种排列方法。
A.24 B.36
C.48 D.60
3.某场乒乓球单打比赛采取5局3胜制。假设甲选手在每局都有70%的概率赢乙选手,若要打满5局,则这场单打比赛甲选手有多大的概率战胜乙选手:
A.0.031 B.0.103
C.0.185 D.0.343
4.某外商计划在四个候选城市投资3个不同的项目,且在同一城市的投资项目不超过2个,则该外商有()种备选的投资方案。
A.36 B.48
C.60 D.64
5.某警卫处有战士24人,随机每3人一班,轮流值班,每6小时换班一次,某3人同值一班后,到下次这3人再同值班,最长需()天。
A.362 B.384
C.506 D.528
6.将3个1,11个0排成一行,使得每两个1之间至少隔着两个0,则共有多少种不同的排法?
A.110 B.120
C.125 D.136
7.单位复印了30份学习资料发放给3个部门,每个部门至少发放9份材料。问:共有多少种不同的发放方法?
A.7 B.9
C.10 D.12
8.某技术部有10名成员,现在需要抽出两个2人小组去解决技术故障问题,共有()种不同的安排方案。
A.1260 B.1440
C.720 D.960
9.某市面上有甲、乙、丙、丁四家企业生产的电热毯,市场占有率分别是:36%、32%、18%、14%,若随机抽出2件电热毯,至少有一件来自乙企业的概率范围是:
A. 0.36-0.48 B. 0.48-0.53
C. 0.53-0.67 D. 0.67-0.74
10.有一办公室有5名职员,其中男职员2人,女职员3人,现随机挑选出2人参加培训,那么至少有一名男职员参加培训的可能性有多大?
A. 60% B. 70%
C. 75% D. 80%
答案解析...请翻下一页哦~
| 2024云南省事业单位备考推荐 | |
| 2024下半年云南事业单位公告预约 | 云南事业单位职位在线查询 |
| 2024云南事业单位全省岗位表下载 | 云南事业单位考试专题信息网 |
| 2024云南事业单位联考图书4本套 | 2024云南事业单位D类4本套 |
| 2024云南事业单位联考必做题库 | 2024事业单位D类必做题库 |

1.【答案】D
【解析】第一步,本题考查概率问题,属于基本概率类。
第二步,“1、2、3、4、5、6”中任选两个数字组成一个两位数,两位数为偶数的话,个位数可能是“2,4,6”,有3种可能;两位数为奇数的话,个位数可能是“1,3,5”,也有3种可能。则这个两位数为奇数的概率和为偶数的概率相同,均为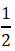 。
。
因此,选择D选项。
2.【答案】C
【解析】第一步,本题考查排列组合问题中的基础排列组合,用分步法解题。
第二步,甲只能坐在两端,有 种方法;再将其余4人排成一排有
种方法;再将其余4人排成一排有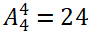 种方法。
种方法。
第三步,则一共有2×24=48种排列方法。
因此,选择C选项。
3.【答案】C
【解析】第一步,本题考查概率问题。
第二步,若要打满5局且甲获胜,则最后一局是甲获胜,前四局选两局获胜共有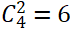 种情况,故概率为0.7³×0.3²×6=0.03087×6=0.185。
种情况,故概率为0.7³×0.3²×6=0.03087×6=0.185。
因此,选择C选项。
4.【答案】C
【解析】第一步,本题考查排列组合问题,属于基础排列组合。
第二步,根据题意,分为两种情况:①投资三个城市,每个城市一个项目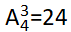 (种),②投资两个城市,其中有一个城市两个项目
(种),②投资两个城市,其中有一个城市两个项目 (种),共有24+36=60(种)。
(种),共有24+36=60(种)。
因此,选择C选项。
5.【答案】C
【解析】第一步,本题考查排列组合问题,属于基础排列组合。
第二步,24人随机选3人值班,共有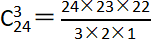 =2024种挑选方法,即有2024种值班小组,已知每6小时换班一次,故一天需要4个值班小组,某三人值班后到下次值班,要想时间最长,则需要将所有值班小组轮流值班一遍,所以最长时间为2024÷4=506(天)。
=2024种挑选方法,即有2024种值班小组,已知每6小时换班一次,故一天需要4个值班小组,某三人值班后到下次值班,要想时间最长,则需要将所有值班小组轮流值班一遍,所以最长时间为2024÷4=506(天)。
因此,选择C选项。
6.【答案】B
【解析】第一步,本题考查排列组合问题,属于方法技巧类,用隔板法解题。
第二步,根据“每两个1之间至少隔着两个“0”,可先将其中两个“0”取出,构成“10101”,剩余9个“0”产生10个空,再将之前伴随有“0”的3个“1”插到9个“0”产生的10个空中,才能保证任意两个“1”之间至少隔着两个“0”,结果为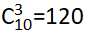 (种)。
(种)。
其中一种情况如图所示:
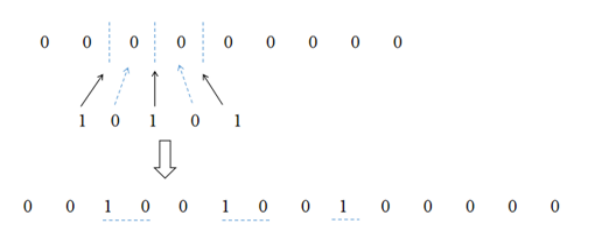

因此,选择B选项。
7.【答案】C
【解析】解法一:
第一步,本题考查排列组合问题,属于方法技巧类,用枚举法解题。
第二步,每个部门至少发放9份材料,从发放数量看有三种分类:(9、9、12),(9、10、11),(10、10、10)。
第三步,对于发放数量(9、9、12),需要确定一个部门发放12份,有3种方法;对于发放数量(9、10、11),各部门发放数量不同,有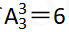 种方法;对于发放数量(10、10、10),只有1种方法。因此共有3+6+1=10(种)不同的发放方法。
种方法;对于发放数量(10、10、10),只有1种方法。因此共有3+6+1=10(种)不同的发放方法。
因此,选择C选项。
解法二:
第一步,本题考查排列组合问题,属于方法技巧类,用隔板法解题。
第二步,每个部门至少发放9份材料,先各部门发放8份,问题转化为:剩余6份放给3个部门,每个部门至少发放1份材料,共有 种不同的发放方法。
种不同的发放方法。
因此,选择C选项。
【拓展】隔板法:n个相同元素,分给m组,至少1个/组,共有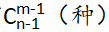 (种)不同的发放方法。
(种)不同的发放方法。
8.【答案】A
【解析】解法一:
第一步,本题考查排列组合问题,属于基础排列组合。
第二步,先从10人中选出4人,再从4人中选择2人进行分组去处理不同的问题,即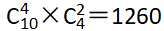 (种)。
(种)。
因此,选择A选项。
解法二:
第一步,本题考查排列组合问题,属于基础排列组合。
第二步,先从10人中选出2人,再从8人中选择2人进行分组去处理不同的问题,即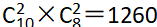 。
。
因此,选择A选项。
9.【答案】C
【解析】第一步,本题考查概率问题,属于分类分步型。
第二步,至少有一件来自乙企业的概率=1-两件都不来自乙企业的概率=1-(1-32%)(1-32%)=0.5376。
因此,选择C选项。
10.【答案】B
【解析】解法一:
第一步,本题考查概率问题,属于分类分步型。
第二步,根据某种情况发生的概率=满足条件的情况数÷总的情况数,可得至少有一名男职员参加培训的可能性有以下两种情况:
①1男1女: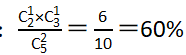 ;
;
②2男0女: ;因为是分类概率,所以总的可能性有60%+10%=70%。
;因为是分类概率,所以总的可能性有60%+10%=70%。
因此,选择B选项。
解法二:
第一步,本题考查概率问题,属于分类分步型。
第二步,根据正向的概率=1-反向的概率,可得至少有一名男职员参加培训的概率=1-没有男职员参加培训的概率,没有男职员即两名均为女职员,代入数据可得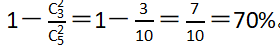 。
。
因此,选择B选项。










