1. 某单位男员工所占比例不足一半，新招聘了8名员工，男员工人数增加了8%，女员工人数增加了6%，问原来该单位男员工比女员工少多少人?

　　A.75

　　B.60

　　C.45

　　D.30

　　2. A、B两船在静水中的航行速度分别为江水中水流速度的3倍和5倍。B船8点从上游的甲码头出发全速行进，中午11点到达下游的乙码头后原路返回。10点30分时，A船也从甲码头出发向乙码头全速行进。问两艘船相遇的点到甲码头和乙码头距离之间的比为?

　　A.5∶4

　　B.7∶6

　　C.3∶2

　　D.4∶3

　　3. 某项工程，若王强单独做，需40天完成;若李雷单独做30天后，王强、李雷再合作20天可以完成。如两人合作完成该工程，王强第一天工作但每工作一天休息一天。问整个工程将会在第几天完成?

　　A.44

　　B.45

　　C.46

　　D.47

　　4. 在一次模拟考试中，小鲁语文、数学、外语和地理四门课的平均成绩是79，他语文、数学、外语地理和历史五门课的平均成绩大于82。如小鲁五门课的成绩都是整数，则他的历史成绩至少为多少分?

　　A.86

　　B.92

　　C.95

　　D.98

　　5. 某单位共有十多名职员，男职员的人数比女职员少40%。该单位要选出先进工作者以及“三八”红旗手各一人(不能是同一人选)，问有多少种推选方案?

　　A.144

　　B.150

　　C.160

　　D.240

　　6. 某公司有38名男员工，27名女员工，现要参加集团组织的羽毛球比赛，如采取自由报名的形式，至少有多少名员工报名才能保证一定能从报名者中选出男女选手各8名参赛?

　　A.65

　　B.46

　　C.35

　　D.16

　　7. 王大妈在市场承包了一个摊位卖水果，一天收摊后清点钱数时，王大妈发现手上有100元、50元和10元的钞票共48张，合计1760元，其中50元比10元多两张，问100元有多少张?

　　A.8

　　B.6

　　C.4

　　D.2

　　8. 一场球赛共有3局，第一局结束后有20%的观众离场，第二局结束之后，剩下的观众中离场的比例比第一局结束时高出5个百分点，此时剩下的观众人数为600人，问球赛开始时有多少名观众?

　　A.900

　　B.1000

　　C.1100

　　D.1200

　　9. 专家对一批刚出土的古代钱币进行鉴定，星期一鉴定了总数的35%，星期二和星期三分别鉴定了前一天剩下的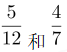，星期四鉴定完了所有剩下的钱币，问这批钱币至少有多少个?

　　A.240

　　B.420

　　C.840

　　D.1680
 

　　10. 火车A过隧道，从车头进入隧道到车尾离开隧道共用时60秒，随后与迎面开来的另一辆火车B相遇，两车速度相同，火车B的长度是A的1.5倍，两车从车头相遇到车尾分开共用时5秒，问火车B从车尾进入隧道到车头离开隧道，要用时多少秒?

　　A.50

　　B.52

　　C.54

　　D.55

　　答案解析...请翻下一页哦~

　　1.【答案】A

　　【解析】解法一：

　　第一步，本题考查基础应用题，用代入排除法解题。

　　第二步，根据男员工人数增加了8%，女员工人数增加了6%，设原来男员工有x人，女员工有y人，所以现在男员工增加了8%x人，女员工增加了6%y人，根据新招聘了8名员工，可得8%x+6%y=8，化简得4x+3y=400;代入A选项，若y-x=75，解得x=25，y=100，刚好符合单位男员工所占比例不足一半，故正确。

　　因此，选择A选项。

　　解法二：

　　第一步，本题考查基础应用题，用数字特性法解题。

　　第二步，根据男员工人数增加了8%，可得：男员工增加的人数=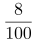×原男员工人数①，化简得：男员工增加的人数=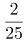×原男员工人数，可得男员工增加的人数是2的倍数;根据女员工人数增加了6%，可得：女员工增加的人数=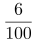×原女员工人数②，化简得：女员工增加的人数=×原女员工人数，可得女员工增加的人数是3的倍数。根据新招聘了8名员工，且男员工所占比例不足一半，可得女员工应增加了6人，男员工应增加了2人，代入①式，原男员工人数为25人，代入②式，原女员工人数为100人，符合题意。

　　因此，选择A选项。

　　2.【答案】A

　　【解析】第一步，本题考查行程问题，属于流水行船类，用公式法解题。

　　第二步，设江水中水流速度为x，所以A、B两船在静水中的航行速度分别3x、5x，根据顺流速度=船速+水速，可得A、B两船在顺流中的航行速度分别4x、6x。根据B船从上游到达下游的时间为3小时，且路程=速度×时间，可得两码头的距离为6x×3=18x;B船到达乙码头后逆流返回，逆流速度=船速-水速，所以返回时B船在逆流中的航行速度为5x-x=4x。

　　第三步，根据A船10点30分出发，可得在B返回时，A已经行驶了30分钟(0.5小时)，行驶的路程为4x×0.5=2x，故11点时，A船与B船的距离为：18x-2x=16x，根据相遇公式：相遇距离=(大速度+小速度)×相遇时间，代入数据得16x=(4x+4x)×相遇时间，所以相遇时间为2小时。A船再行驶2小时的路程为2×4x=8x，B船再行驶2小时的路程为16x-8x=8x，所以此时相遇的点到甲码头和乙码头距离之间的比为(2x+8x)∶8x，化简得5∶4。

　　因此，选择A选项。

　　3.【答案】B

　　【解析】第一步，本题考查工程问题，属于效率类，用赋值法解题。

　　第二步，设王强的效率为x，李雷的效率为y，根据工作总量不变，可得：40x=30y+20(x+y)，化简得2x=5y，赋值王强的效率为5，李雷的效率为2，所以工程总量为40x=200;若两人合作，根据王强每工作一天休息一天，可得每天两人的效率和呈现以下的周期性：(7，2)，(7，2)，(7，2)，……，每两天可看作一个周期，共完成7+2=9(个)工作量，根据200÷9=22…2，可得22个整周期即44天，此时还剩余2个工作量并由两人合作完成(不到1天)，所以工程将会在第45天完成。

　　因此，选择B选项。

　　4.【答案】C

　　【解析】解法一：

　　第一步，本题考查基础应用题，用方程法解题。

　　第二步，设历史成绩为x分，根据“五门课的平均成绩大于82”，可得79×4+x>82×5，解得x>94。由于小鲁五门课的成绩都是整数，结合选项，至少为95分。

　　因此，选择C选项。

　　解法二：

　　第一步，本题考查基础应用题。

　　第二步，若现在平均分为82，那么每科的分数要比原来多82-79=3(分)，所以五科要比原来多3×5=15(分)，历史的分数为79+15=94(分)，根据五门课的平均成绩大于82分，且每门课的成绩都是整数，所以历史的分数应大于94，结合选项，至少为95分。

　　因此，选择C选项。

　　5.【答案】B

　　【解析】第一步，本题考查排列组合问题，属于基础排列组合。

　　第二步，根据男职员的人数比女职员少40%，设女员工有x人，则男员工有x×(1-40%)=0.6x，所以总人数有1.6x，根据单位共有十多名职员，且人数均为整数，所以x只能为10。因此，女职员有10人，男职员有6人。

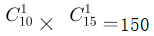　　第三步，根据要选出先进工作者(男女均可)以及“三八”红旗手(女)各一人，可先从10个女职员选出一个“三八”红旗手：，再从剩下的15人中选出一个先进工作者：，即推选方案数为(种)。

　　因此，选择B选项。

　　6.【答案】B

　　【解析】第一步，本题考查最值问题，属于最不利构造，用公式法解题。

　　第二步，根据“至少……保证……”可知本题为最不利构造问题，可根据固定步骤：答案=最不利值+1求解。本题的最不利情况为：男员工离“8名参赛”差1人或女员工离“8名参赛”差1人。分析可知，由于男选手人数较多，则当38名男选手全部选出且女选手只选出7名时为最不利的情况，即最不利值=38+7=45;

　　第三步，接下来只需再选一人，即可满足保证一定能从报名者中选出男女选手各8名参赛。答案=45+1=46。

　　因此，选择B选项。

　　7.【答案】C

　　【解析】第一步，本题考查基础应用题，用方程法解题。

　　第二步，设100元有x张，50元有y张，10元有(y-2)张，列方程组得：x+y+(y-2)=48①，100x+50y+10(y-2)=1760②，解得x=4，y=23。

　　因此，选择C选项。

　　8.【答案】B

　　【解析】解法一：

　　第一步，本题考查基础应用题，用方程法解题。

　　第二步，设球赛开始时有10x名观众，根据“第一局结束后有20%的观众离场”，可知剩下的观众为8x;根据“第二局结束之后，剩下的观众中离场的比例比第一局结束时高出5个百分点”，可知第二次离场人数为：8x×25%=2x。

　　第三步，两局结束，剩余观众人数为10x-2x-2x=6x，即6x=600(人)，解得x=100(人)，所以球赛开始时观众为10×100=1000(人)。

　　因此，选择B选项。

　　解法二：

　　第一步，本题考查基础应用题，用赋值法解题。

　　第二步，赋值球赛开始时观众人数为100，第一局结束剩(1-20%)×100=80;第二局离场比例为20%+5%=25%，则剩下观众人数为(1-25%)×80=60。此时，剩下的观众人数为600人，则开场时总人数为600÷60×100=1000(人)。

　　因此，选择B选项。

　　9.【答案】A

　　【解析】解法一：

　　第一步，本题考查基础应用题，用数字特性法解题。

　　第二步，根据题目进行分析：

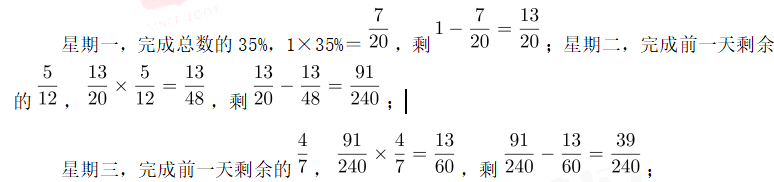
　　因此，星期四完成了总数的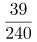。由于钱币个数为整数，因此钱币总数是240的倍数，排除BC项。因此，这批钱币至少有240个。因此，选择A选项。解法二：第一步，本题考查基础应用题，用代入排除法解题。第二步，题目问“这批钱币至少有多少个”，从最小的选项开始进行代入排除：代入A选项，这批钱币至少有240个，具体情况如下：

　　星期一鉴定了240×35%=84个，剩240-84=156个;星期二鉴定了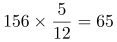个，剩156-65=91个;

　　星期三鉴定了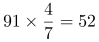个，剩91-52=39个;则星期四鉴定39个，满足所有题目要求，即这批钱币至少有240个。因此，选择A选项。

　　10.【答案】A

　　【解析】解法一：

　　第一步，本题考查行程问题，属于相遇追及类，用方程法解题。

　　第二步，设隧道长为L，火车A长度为x，则火车B长度为1.5x。火车A过隧道时的速度为：(x+L)÷60。火车A和B相向而行，根据相遇问题公式，两车的速度和为：(x+1.5x)÷5=0.5x，由于两车速度相同，则每辆车的速度为0.5x÷2=0.25x。因此，(x+L)÷60=0.25x，L=14x。

　　第三步，设火车B从车尾进入隧道到车头离开隧道用时为t，利用两车速度相同可得：(x+14x)÷60=(14x-1.5x)÷t，解得t=50(秒)。

　　因此，选择A选项。

　　解法二：

　　第一步，本题考查行程问题，属于相遇追及类，用赋值法解题。

　　第二步，根据“火车B的长度是A的1.5倍”赋值，B的长度是3，A的长度是2，二者和为5。AB两车从车头相遇到车尾分开共用时5秒，两车做相遇运动，且速度相同，根据相遇问题公式，2×火车速度×时间=A火车长度+B火车长度，2×火车速度×5=3+2=5，可理解为两倍火车速度通过5的距离用5秒，则单倍火车速度通过5的距离用10秒，故60秒将通过30的距离，可理解为火车A从车头进入隧道到车尾离开隧道共用时60秒，则(隧道+A火车长度)是30，所以隧道长度30-2=28。

　　第三步，现在B从车尾进入隧道到车头离开隧道行使距离为28-3=25，则(隧道-B火车长度)∶(隧道+A火车长度)=25∶30=5∶6，由于两车速度相同，则时间之比就是路程之比，则火车B所用时间为60×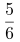=50(秒)。

　　因此，选择A选项。